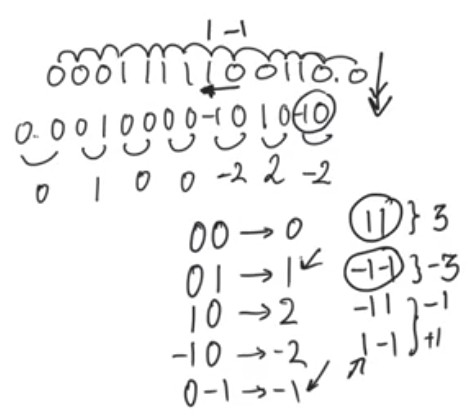Booth recoding

source this playlist on arithmetic circuits.

Introduction

• The difference between a full multiplier and a constant multiplier is that there are specific mutliplier operands were particularly easy to multiply by
• specifically those multiplier operands that are powers of two like 4,16,32, …
  • The reason these operands are particularly easy is that they only have a single 1 and the remainder of their bits is null (0)
  • So when we expand the summands we find that we only have one active summand and the rest are trivial,
  • so we don’t have to do any additions, we end up shifting the mutlipland by as many bits as the active bit location in the multiplier
  • This happens when we have long string of zeros in the multiplier operand which allows us to trivialize most of the summand

Booth recoding algorithm

• Allows us to benefit from long strings of ones not just zeros
• The worst case in a multiplier is to be all ones (all M bits are ones), cause that means it has all active summands
  • The hard way is to add the multiplicand M shifted times as a summand
  • The easy way is to recognise that all ones simply means -1 in twos complement, and the result of this is simply (- the multiplicand)
• The booth recoding algorithm recognizes that long strings of ones can be represented in two’s complement as -1
• It utilizes this by recoding multiplier operand to remove long strings of ones and reduces them to long strings of zeros
• This can also be applied if the long strings of ones are in the middle of the multiplier and even if we are using unsigned numbers

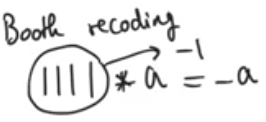
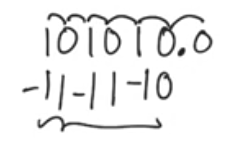
Example of ones in the middle

• 101110 have 111 in the middle = 7, in thier position 1110 = 14
• 1110 can be recoded so that the higher bit position = 1, then we have 00 and -1 at the LSB of the string of one then the last zero 0 (100-10)
• now we are using not a binary but a trinary representation of numbers where each bit can be represented as -1, 0, 1
• This is useful because we have reduced the number of the active ones in the multiplier operand by compressing the sequence of ones into a sequence of -1,0,1

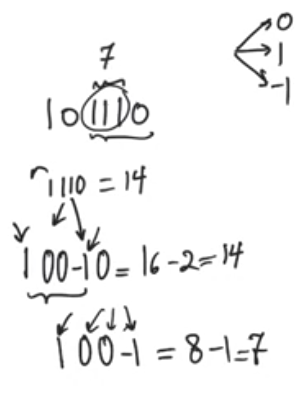
Recoding systematically

• Cover overlapping pairs of bits within the multiplier operand
• whenever you see 00 you interpret this as a zero
  • 01 you interpret this as a 1
  • 10 you interpret this as a -1
  • 11 you interpret this as a 0
• we always begin by adding a zero before the binary point even if the number is purely integer
• we look at the pairs of bits, and we always look at each bit twice
• if you don’t have enough bits on the MSB side you should sign extend so that you have an even number of bits
• Why does this translation makes sense?
  • if we see a 00 in the pairs of bits that means we are moving through a string of zeros, therefore that gets interpreted as a zero
  • if we see a 01 means we are exiting the string of ones, and according to the example, when you are exiting the string of ones, you have to add a one at the highest MSB to compensate for the -1 at the LSB, therefore that gets interpreted as a one
  • if we see a 10 in the pairs of bits that means we are Entring the string of ones, which means you add a -1 to the LSB
  • if we see a 11 means we are within a string of ones, which after booth recoding it’s reinterpreted as a string of zeros, so pairs of ones are interpreted as a zero
• We add a zero before the binary point cause if you have a 1 as a LSB you need a 0 before it to allow you to interpret properly

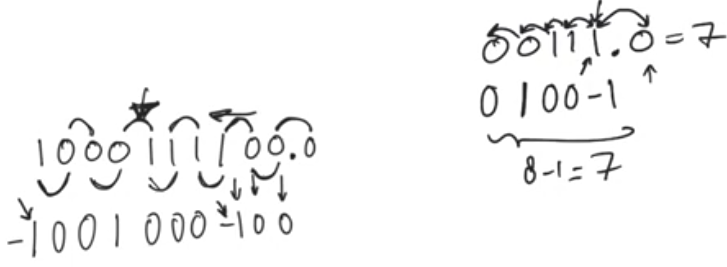
Worst case

• Without booth recoding the worst case was all ones, but now it’s nearly the best case after all zeros
• The worst case with booth recoding is if you have alternating ones and zeros
• We end up with more nontrivial summands than we had in the origianl operand
• This means the booth recoding doesn’t always work to reduce the number of non trivial summands
• But statistically it’ll work, cause in large number it’s alot less likely to see numbers with alternating ones and zeros then to see blocks of zeros and blocks of ones

Modified Booth recoding

Introduction

• Mutliplying N bits multiplier by M bits multiplicand
• Convert radix 2 multiplicands (M bits) to radix 4 (becomes M/2 bits)
• Using this we can reduce the number of summands that we produce out of multiplication, which could greatly influence the complexity of the multiplier
• in the multiplication instead of shifting the summands one bit to the left we shift 2 bits to the left
• Instead of having M summands we now have M/2 summands which reduces the number of additions that we have to use
• There is a hidden complexity which is the complexity of calculating the partial products
  • in the example multiplying by 3 is equivalent to shifting then adding
  • which means that we are implicitly within calculating the partial products, we are doing another summand addition
  • so we haven’t actually reduced the complexity of anything
• On the other hand if we first encode the multiplicand operands then we reach something very useful called the modified booth algorithm

Modified booth algorithm

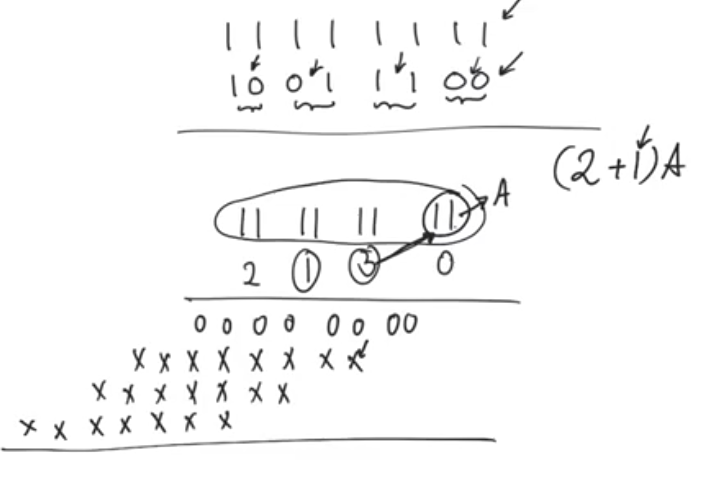
• Do normal booth recoding
• Take pairs of bits without overlapping and do sign extend if needed, and convert to radix 4
• The possibilties that comes from covering pairs of bits here are 0, -1, -2, 2
  • 0 trivial
  • -1 two’s complement
  • 2 shift to the left
  • -2 shift to the left and a two’s complement
• So you don’t need to calculate partial productes that are any more complicated than the partial products you normally calculate
• The rest of the cases can never be seen if you do booth recoding first
  • you can’t see a -1-1 because -1 means you are entring a string of ones, so you can’t enter another string of ones without exiting the first one
  • you can’t see a 11 because 1 means you are exiting a string of ones, so you can’t exit another string of ones without entering.