Carry bypass adder

source this playlist on arithmetic circuits.

Ripple carry adder

• Ripple carry adder is an adder whose delay increased in an order of N O(N)
• The delay is linearly dependant on the number of bits

Introduction

• Carry bypass adder wouldn’t be possible without the generate propagate logic
• makes a very simple observation
  • if we have an N-bit adder, the final carry out doesn’t have to be calculated if every bit position within the adder is propagating
  • Carry out doesn’t have to be calculated and can be bypassed from Carry in
• so we can multiplex the Cout’s source to be from Cin if all bit postitions are propagating
• it’s still a ripple carry adder cause the critical path (worst case) doesn’t improve

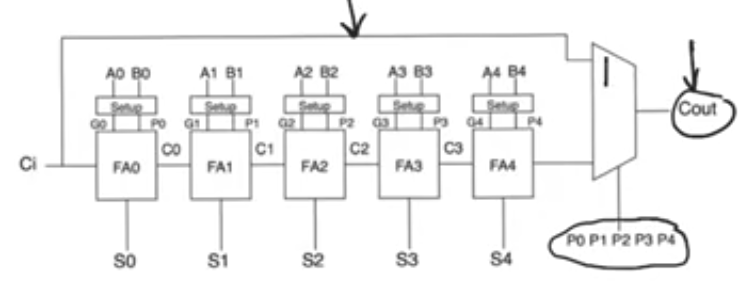
• A true carry bypass adder doesn’t take this shape but it still informs of how to design a carry bypass adder

Carry bypass adder

• A true carry bypass adder consists of multiple blocks similar to the one above
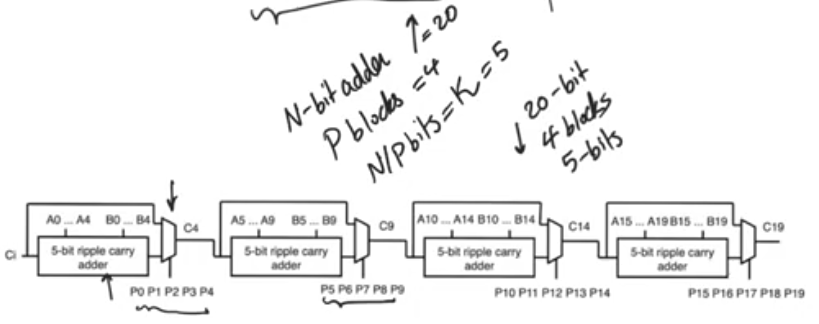
• for a 20 bit adder, it consists of 4 blocks of 5 bit carry bypass adder

• For an N bit adder consists of P blocks each block with N/P=k bits

• 

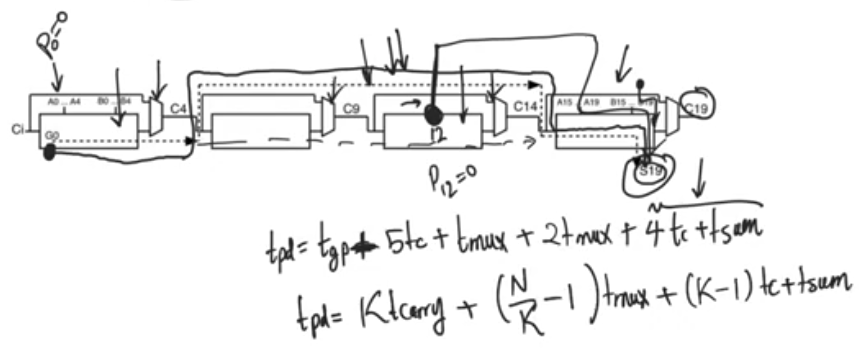
Critical Path

• the critical path passes through the first ripple carry adder, then (N-2) intermediate blocks bypass path then the last ripple carry path till the last sum bit

WHY the critical path bypasses the intermediate blocks?

• In any block if you have to go through the ripple carry path, then that means that the MUX’s selector is not equal to 1
• which means that the product of all propagates isn’t equal to 1
• which means at least one of the propagate bits is not equal to 1
• if at least one of the propagates in not equal to 1 then that means at least one generate or delete in the path is equal to 1 as they are mutually exclusive
• this means somewhere in the ripple carry path, some bit is generating or deleting
• so in the N-bit adder if we assume that some bit in an intermediate block isn’t equal to 1, this means that the bit in this position is either generating or deleting a carry
• but if you go back to the definition of generate and delete they mean that the carry out can be calculated without waiting for the carry in
• so this means that this position have the carry out bit without waiting for the carry in coming from the previous position
• this means that the path starts from this bit, and this can’t be the critical path cause it’s a very short path
• so we find that the lognest critical path is for the bit at position 0 to be generating or deleting and then every other bit is propagating even in the last block
• otherwise if some bit other than bit 0 is generating or deleting then the path starts from this bit which is shorter than the critical path
• In the critical path the last block is propagating, but for the critical path we take the output at the last sum bit which takes longer then Cout.
• so the propagation delay Tpd = K Tcarry + (N/K-1) Tmux + 4Tc + Tsum

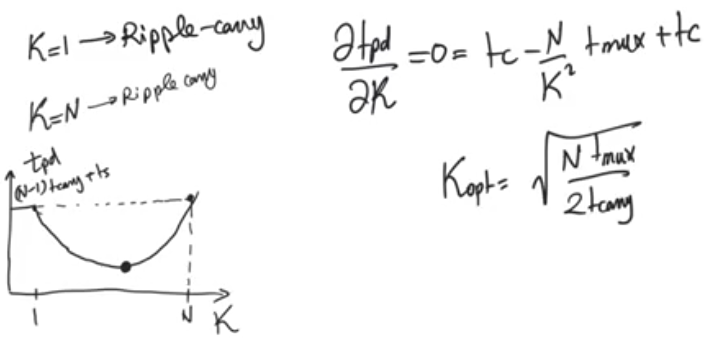
Optimizing delay

• This delay is linear O(N/K) instead of O(N) which is some improvement than the ripple carry adder
• if you look at this you would think that increasing K(number of bits per block) as much as possible is good
• but the intercept with y, the initial delay depends on 2*k so increasing K increases the intercept

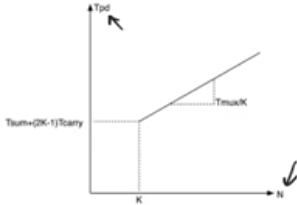
• so the K value for optimal delay can be calculated by differentiating with the delay with respect to K