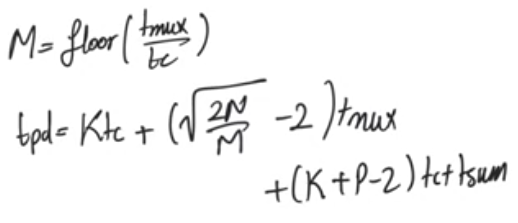Carry select adder

source this playlist on arithmetic circuits.

Introduction

• It was popular when the silicon area was considered cheap relative to needed performance, still pretty much true
• it sacrifice area to get performance
• Divide a large adder into smaller blocks
• each block waits for the carry bit from the previous block which could be either 0 or 1
• so what if we have two ripple carry chains per block, and each of them assuming that the carry bit coming from the outside is either 0 or 1
• this allows this carry chain to calculate all its sums and all its carrys but for every position it’s gonna calculate two sums and two carrys
• so every block doesn’t have to wait for the previous carry, it can calculate and when the carry comes it selects the correct result using a mux

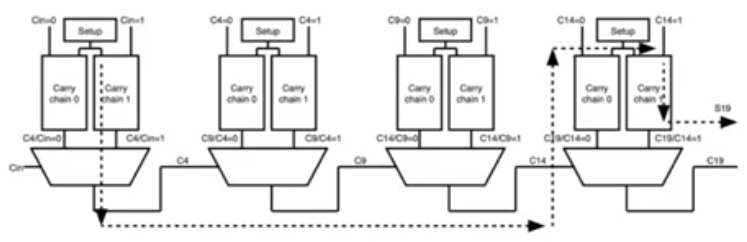
Critical path

• the critical path is gonna pass through the first ripple carry path
• and from then on it’s gonna pass through the multiplexers in the middle
• till it reaches the last block where it has to pass through the whole carry chain
• for every block when the first adder finishes all blocks’ adders would have finished, and we gonna add the muxes delays
• for the last block we are intersted in the Sum bit so we have to wait for the carry chain of the last block

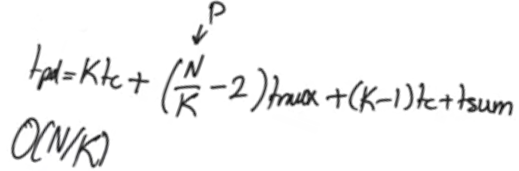
optimize to obtain sublinear delay behaviour

• All the blocks results are ready at the same time
• we don’t use a block’s result until a number of multiplexers delays, depending on the block’s location
• blocks down the road wait for more muliplexers’ delays than the earlier ones

• so we can make the blocks down the road larger then the earlier ones (number of bits per block)
• assuming the multiplexer delay = carry delay Tmux = Tcarry
• we get square root dependance on N the number of bits

• In case multiplexer delay is not equal to carry delay Tmux != Tcarry
• The square root dependance on N too