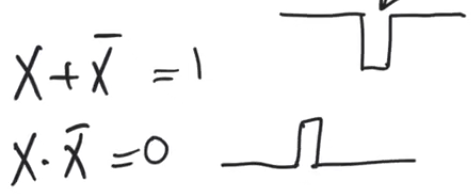Static hazards

• Source this playlist on Testing.

Static 1 hazards

• Identify static one hazards and solve them using K-map approach
• Static 1 hazards always reduce to the simple form of
  • two paths that reconvene at an OR gate
  • and these two paths have to have differential delay
  • and they have to present the OR gate with some form of true and inverted form of a certain variable
• When that happens you’ll possibly see a static 1 hazard
  • depending on the delays of the circuits and the inertial modle delay used

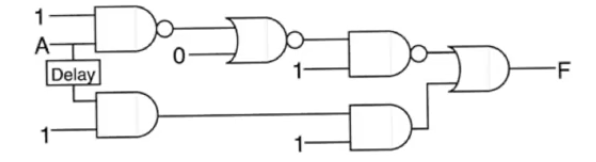
Example

• The previous form doesn’t have to be explicitly exist in a circuit to have a static 1 hazard
  • it could be implicitly present
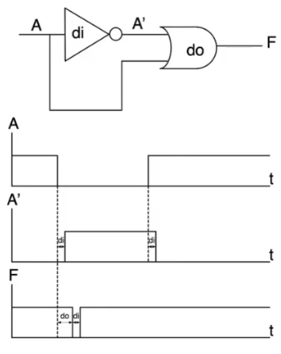
• The circuit in the example has a static 1 hazard
• Variable A has two path to the final OR gate
  • This isn’t enough for a static hazard to occur
  • There also has to be an inversion between these two variables
• The inversion of A happens using the NAND gates in the upper branch
• The third condition is that the two branches has differential delay so that you can have a time through which the glitch appears
  • this is obvious in this circuit because the upper branch is much longer than the lower branch
• The values for other inputs to the circuit are the values that will cause the glitch to appear
  • The glitch doesn’t appear in all conditions under all circumstances
  • It only appears under certain conditions

Solution

Combinational delay

• Static hazard occurs because we see a true and a complement form of a variable having differential delays
• The glitch occurs when the variable makes a transition and there is a period of time in the middle where neither of A or A' are 1, thus we see a glitch with a value of 0
• If we compensate the differential delay by adding a delay to the lower path so that both paths’ delays are equal
  • Then A and A' are gonna match exactly
  • If that happens, there is no space for the glitch to occur
• This delay has to be combinational delay
  • Absolute time measured in terms on nano seconds
• It’s extermly difficult to match combinational delays, so it’ll be extermly difficult to match the delays of the branches exactly
• This approach isn’t very practical

K-map approach

• The correct approach is to add extra combinational logic which masks the offending transition
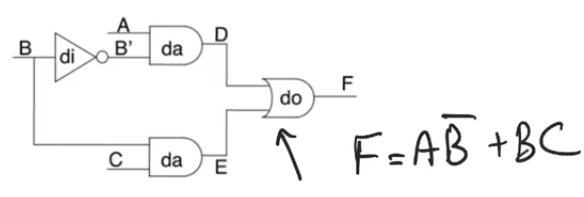
• Going back to the original circuit F=AB'+BC

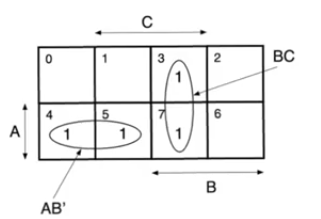
• The K-map has 8 squares each one represent the min terms
• The function has active min terms 3,4,5,7
• Static 1 hazard happens when A=1 and C=1
  • If be makes a transition between squares 5 and 7 the glitch happens
  • for min terms m5<->m7 we have a glitch where the only variable changes is B
  • these min terms are adjacent and not covered by a group

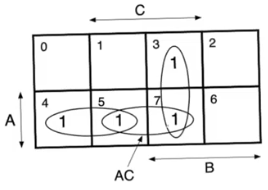
• The solution is to cover these min terms by a group
• This additional term is AC
• This is a redudant covering that doesn’t change the logic function
• It’s additional hardware that will solve the static 1 hazard and completely mask it

• In the original problem when we make a transition between min terms m5<->m7 the function is supposed to keep F=1
  • in m5 we are relying on the term AB' to maintain the value of 1
  • in m7 we are relying on the term AC to maintain the value of 1
  • But C and A aren’t the variables that give us the 1 at the nodes D and E, B and B' are
  • because there is a differential delay between B and B' then there will be a period of time where neither B nor B' are ones and therefor you’ll see a glitch
• When adding the term AC we now have a term where when both A and C equal to 1 this term is also 1

Static 0 hazards

• similar to static 1 hazards in terms of structure and solution
• Static 0 hazards reduce to the simple form of
  • two paths that reconvene at an AND gate
  • and these two paths have to have differential delay
  • and they have to present the AND gate with some form of true and inverted form of a certain variable
• Variable A made two transisitions 1->0 and 0->1, the glitch only appeared when it made a transition from 0->1

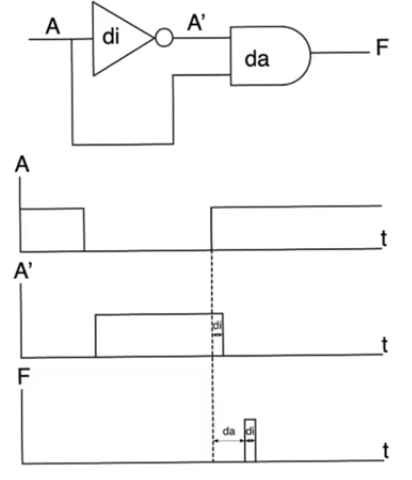
Example

• The previous form doesn’t have to be explicitly exist in a circuit to have a static 1 hazard
• Variable A has two path to the final AND gate
• The inversion of A happens using the NAND gates in the upper branch
• There is a differential delay between the bottom and the top branches because the upper branch is much longer than the lower branch
• The values for other inputs to the circuit are the values that will cause the glitch to appear
  • The glitch doesn’t appear in all conditions under all circumstances
  • It only appears under certain conditions

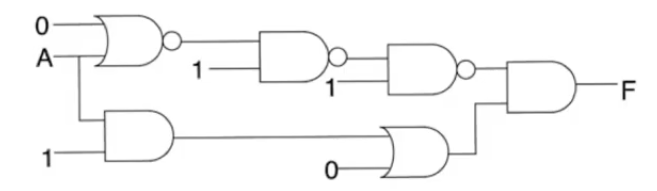
Kmap approach

• This is a POS (product of sums) circuit, the variable which will cause the static hazard is variable B
• The output is F=(A+B)(C+B') which allows us to observe a glitch if B makes a transition 0->1
• For POS circuits when you suspect there is a static 0 hazard, it’s better to represent the circuit on the Kmap using zeros rather than one
  • circuit represented using max terms
• The active max terms are m0,m1,m2,m6
• The glitch happens at two adjacent 0 squares which are not covered by a group
  • The kmap has adjacency on the edges
• Sqaure m2 and m0 are adjacent
  • any transition between them represent a glitch
  • The only variable that makes a transition between them is B

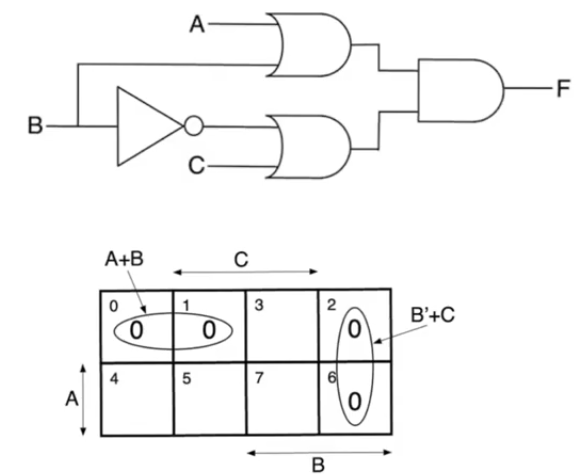
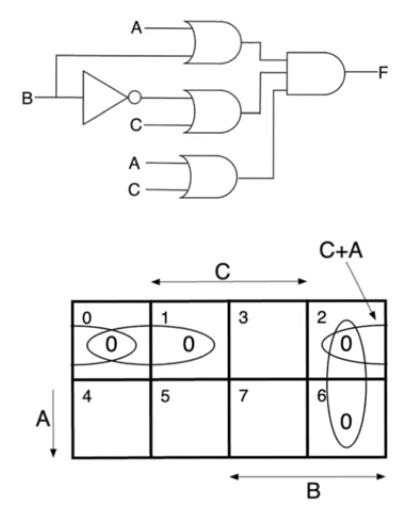
• This problem is solved by covering the uncovered transition with a redundant term C+A

Static hazards in logic equations

• The kmap approach towards detecting and solving static hazards is very limiting
  • it doesn’t give any way to deal with dynamic hazards
  • it only allows you to deal with functions with up to four variables
• The best way to detect and solve hazards static or dynamic is to look at logic expressions and try to work from them
• When you are looking at an equation you are looking for an expression in the form X+X' or X.X'
  • These are terms that indicates the possibility of a hazard
  • X+X' is always equal to 1 and because there could be a differential delay between the X and X' there is a possibility that there will be a glitch (static 1 hazard)
  • X.X' is always equal to 0 and because there could be a differential delay between the X and X' there is a possibility that there will be a glitch (static 0 hazard)

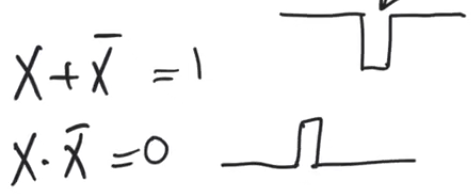
Example

• Function Z=AB(C+DE')+F(GH+EK)
• In this expression the only variable that has the potential to have a hazard is variable E
  • as it’s the only variable that makes an appearance in its true and complement form
• We need to know what other variables’ values brings up the glitch to know whether it’s a static 0 or 1 hazard
  • We have to think what they have to be at inorder to allow E and E' to meet together
• All variables that are multiplied (ANDed) E or E' have to be 1 inorder to make it propagate A=B=F=K=D=1
• All variables that are added (ORed) E or E' have to be 0 inorder to make it propagate C=0
  • G and H we need only on of them to be equal to 0
  • They can be GH=0X or GH=X0
• In that case Z=E'+E so we have a static 1 hazard
• To solve this glitch we add another product them that keeps the value of Z at one in this condition
  • Z=AB(C+DE')+F(GH+EK)+ABFKDC'GH'
  • This additional term solves the static hazard
• there could be multiple sources of hazards in which case you will deal with each variable independently

Static hazards in complex circuits

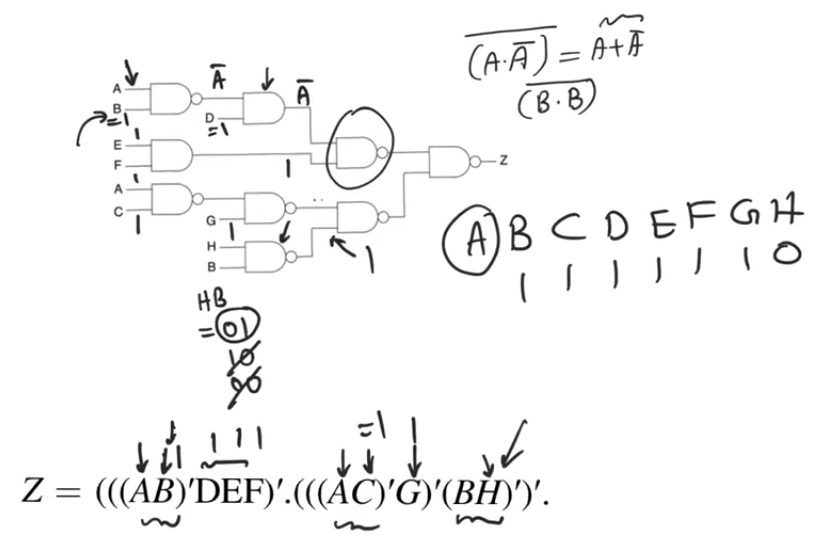
• for a static hazard to occur we have two at least two appearances for a variable
  • All the input variables that have a single appearance don’t have a potential to cause a glitch
• In the example the only variables that could cause a glitch are A and B cause they both appear twice

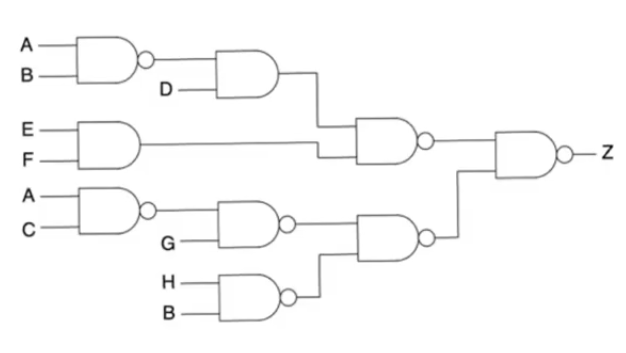
• For A the gate in which both occurences appear is the final NAND gate, we have to check the other static hazard conditions
  • The upper branch A appearance passes through the first NAND gate to be A', then A' for the next AND gate, then it’ll make an appearance as A after the second NAND gate
  • The bottom branch A it’ll make an inversion through the NAND gate then another inversion through the second NAND gate, then a third inversion so it’ll be A'
  • So both meet at the final nand gate as A and A'
  • so they have a potential to cause a hazardif they have differential delay
    • which is a possibility here cause the top path goes through two NAND gates and AND gate
    • The bottom one goes through three NAND gates
  • A will cause a static 1 hazard
    • at the final NAND gate we have Z=(A.A')' which is by demorgan’s theorem equals Z=A+A'
• For B the both appearances meet at the final NAND gate
  • The upper branch will be B' then B' Then B after the two NANDs and the AND gate
  • The bottom branch will be B' then B after passing through the two NAND gates
  • so it makes a transition and meets at the final gate as (B.B)' this isn’t gonna cause a static hazard
• so just because a variable has a couple transition through the circuit doesn’t mean you’ll have a hazard because of it
  • you also need a true an a complement form meeting at a certain gate

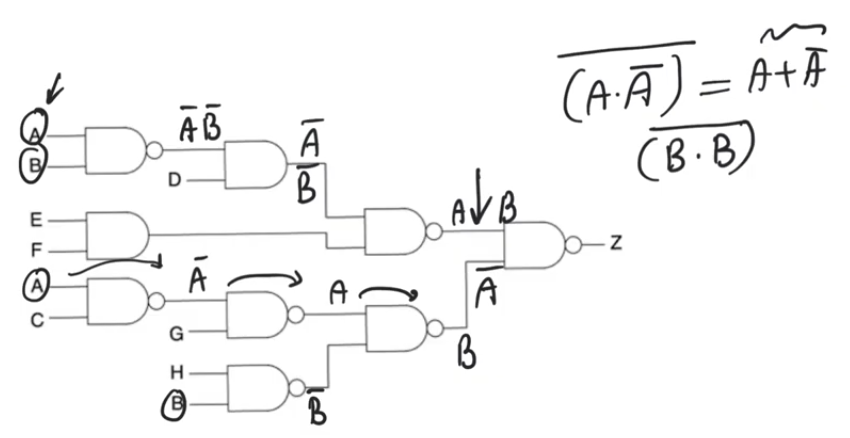
• The circuit expression is Z=(((AB)'DEF)'.(((AC)'G)'(BH)')', we need to get the input variables other than A that will bring us the glitching structure Z=A+A'
• First NAND gate has to have B=1 to allow A to propagate
• Then D=1 to allow A' to propagate through the AND gate
• E=1 and F=1 to allow A' to propagate through the NAND gate to prevent them from masking the output to zero
• C=1 to allow A to pass through the NAND gate and G=1
• Finally either of H or B has to be equal to 0 to output a 1 from the NAND gate to allow the A to propagate, BH=00,01,10
  • But in the top branch we force B=1, which doesn’t allow us to use any combination except for BH=10
• so the final combination that show the glitch is ABCDEFGH=X1111110
  • The gltich appears because for this combination regardless of the value of A we should have an output equal to Z=1
  • however for this transition we are relying on A to keep the function equal to 1
• The glitch is removed by adding a product term that’s gonna be 1 for this input variables combination BCDEFGH'
• Z=(((AB)'DEF)'.(((AC)'G)'(BH)')'+BCDEFGH'